Introduction
APM 50179 EP

Loic Gouarin
- Research engineer in scientific computing at CNRS since 2005
- Joined CMAP in 2018
- Co-author of pylbm, samurai, xtensor-sparse, xeus-cling

Johan Mabille
- Scientific software developer, Quant developer, formerly quant developer at HSBC
- Joined QuantStack in 2016
- Co-author of xtensor, xtensor-sparse, xsimd, xeus, xeus-cling
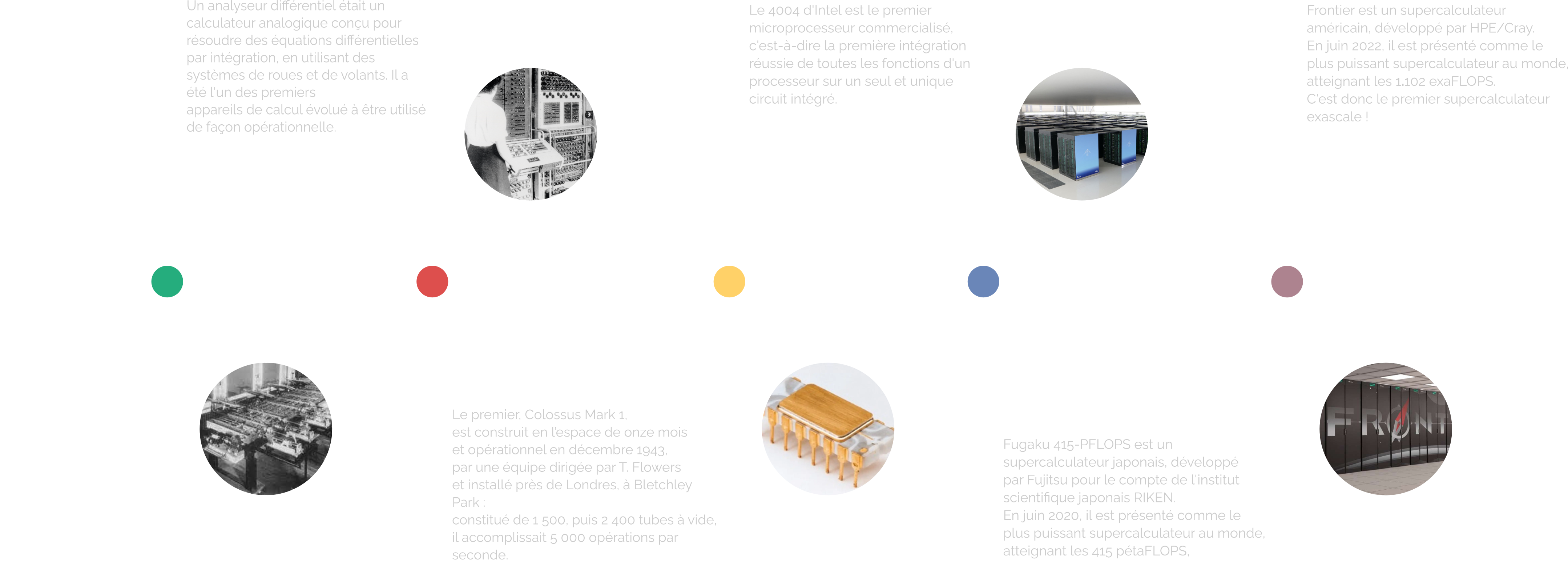
The evolution of computing

The evolution of computing
The evolution of computing
The evolution of computing
The evolution of computing
Heterogeneous architectures
-
CPU
- X86
- ARM
-
Accelerators
- GPU
- FPGA
- VE
The complexity is everywhere
The scientific software today
The languages
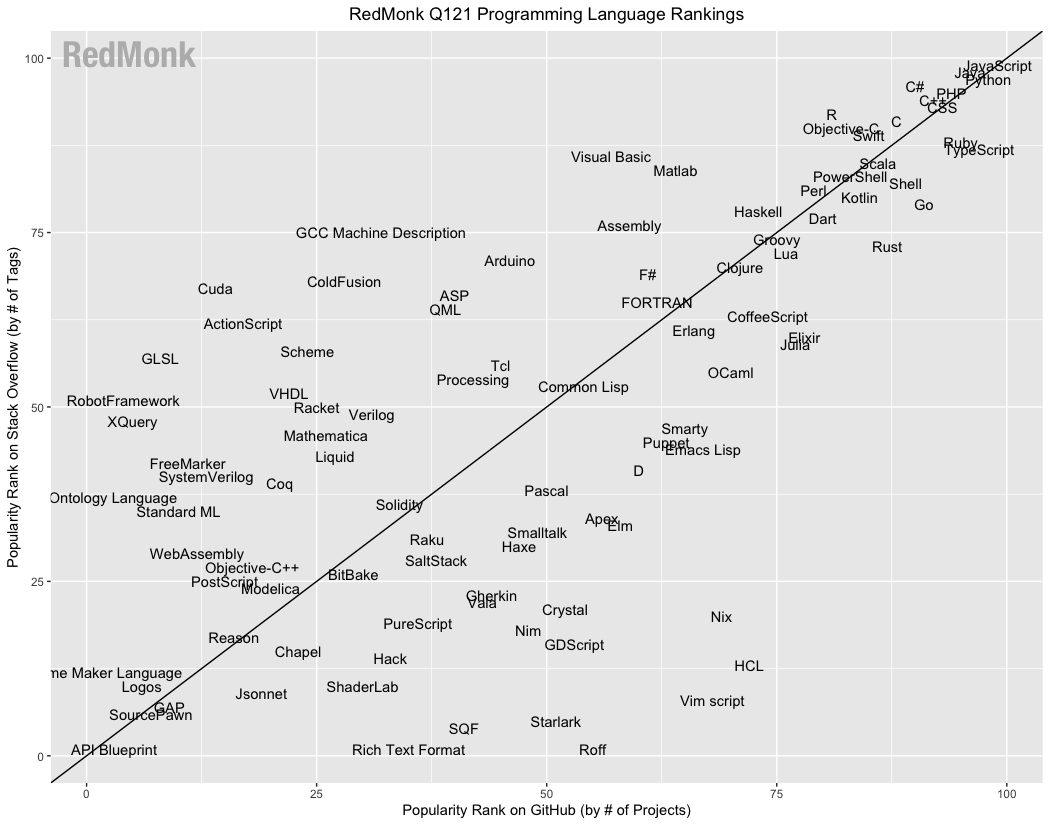
Today there are thousands of languages.
And some of them are of interest for scientific computing.
Interpreted vs compiled
Interpreted language
- Source code is executed line by line by an interpreter.
- Errors occur at runtime, unless they are syntax errors.
- Allow to prototype easily and quickly.
- Deliver relatively slower performance.
- Example: Python, Bash, JavaScript, Lua
Compiled language
- Source code is converted into machine code.
- The compilation process prevents several errors.
- It takes time to set up and run the compilation for each change.
- Deliver better performance.
- Example: C, C++, Fortran
Best way to learn a new language
- Learn the vocabulary
- Practice
- Read the source code of well known Open Source software
- Practice
- Practice
- ...
Open source components
Building a community around software takes time.
The implementation of these components is a guarantee of reliability and confidence.
Open Science

During this course
We will see
C++ basics
APM 50179 EP
C++ origins
- 1982: Bjarne Stroustrup started to develop a successor to C: the C++
- 1985: the first edition of The C++ Programming Language was published
- 1989: C++ 2.0 was released, followed by the second edition of The C++ Programming Language
- 1998: C++98 was released
- 2003: C++03 was released (with minor changes)
- 2011: C++11 was released
- 2014: C++14 was released
- 2017: C++17 was released
- 2020: C++20 was released
- 2023: C++23 will be released
Interesting links
- C++ Core Guidelines: some guidelines to write better modern C++ from C++14 and later
- cppreference: very nice reference on the use of C++ in all version
- cppcon: annual C++ conference
- C++now: another annual C++ conference
- isocpp: website with a list of articles, event, training, ... about C++
A first program
#include <iostream>
#include <cmath>
int main(int argc, char* argv[])
{
double x1 = 1., y1 = 0.;
double x2 = 0., y2 = 1.;
double distance = std::sqrt((x2 - x1) * (x2 - x1) + (y2 - y1) * (y2 - y1));
std::cout << "distance = " << distance << std::endl;
return 0;
}
A first program
#include <iostream> // #include imports functions not built in the language
// but defined in header files
#include <cmath> // More generally, # starts a preprocessor directive
int main(int argc, char* argv[]) // Each executable program must have a function called main.
{ // The body of a function is delimited with curly braces (scope)
double x0 = 1., y0 = 0.; // Declaration and initialization of variables x0, y0, x1 and y1.
double x1 = 0., y1 = 1.; // C++ is a statically typed language
// std:: is a namespace qualifier
double distance = std::sqrt((x2-x1)*(x2-x1) + (y2-y1)*(y2-y1));
// Writing is done with the output operator <<
std::cout << "distance = " << distance << std::endl;
return 0; // Return value of the main function (declared to return an int)
} // Closes the body (scope) of the function
Variables
C++ is a statically typed language
- Variable must be declared with a type
- This type is final and cannot be changed after the declaration
- Declaration (and initialization) of variables have the following scheme:
type variable_name;
type variable_name = value;
type variable_name1 = value1, variable_name2 = value2, ...;
Built-in types
- character types
- boolean
- integers
- floating-point types
- C-style arrays
Character types
- signed char (1 byte = 8 bits)
- unsigned char (1 byte = 8 bits)
- char (equivalent to signed or unsigned, but distinct)
- wchar_t (system dependant, generally 2 or 4 bytes)
- char16_t (2 bytes = 16 bits)
- char32_t (4 bytes = 32 bits)
Character types
const char* c = "character_string";
char s[17] = "character_string";
Prefer std::string over arrays of characters
std::string s = "character_string";
Booleans
- bool (1 byte = 8 bits)
- 2 possible values, true or false
bool b1 = true, b2 = false;
std::cout << std::boolalpha <<"b1: " << b1 << std::endl;
std::cout << "b2: " << b2 << std::endl;
Integers
- (unsigned) short (at least 2 bytes = 16 bits)
- (unsigned) int (at least 4 bytes = 32 bits)
- (unsigned) long (at least 4 bytes = 32 bits)
- (unsigned) long long (at least 8 bytes = 64 bits)
- std::size_t (8 bytes = 64 bits)
- std::ptrdiff_t (8 bytes = 64 bits)
C++ standard also guarantees
1 == sizeof(char) ≤ sizeof(short) ≤ sizeof(int) ≤ sizeof(long) ≤ sizeof(long long)
| types | size in bytes | lower bound | upper bound |
|---|---|---|---|
| short | $2$ | $-2^8$ | $2^8 - 1$ |
| unsigned short | $2$ | $0$ | $2^{16}$ |
| int | $4$ | $-2^{16}$ | $2^{16} - 1$ |
| unsigned int | $4$ | $0$ | $2^{32}$ |
| long long | $8$ | $-2^{32}$ | $2^{32} - 1$ |
| unsigned long long | $8$ | $0$ | $2^{64}$ |
#include <limits>
#include <iostream>
int main(int argc, char* argv[])
{
std::cout << "short: " << sizeof(short) << " "
<< std::numeric_limits<short>::min() << " "
<< std::numeric_limits<short>::max() << std::endl;
std::cout << "int: " << sizeof(int) << " "
<< std::numeric_limits<int>::min() << " "
<< std::numeric_limits<int>::max() << std::endl;
std::cout << "long: " << sizeof(long) << " "
<< std::numeric_limits<long>::min() << " "
<< std::numeric_limits<long>::max() << std::endl;
std::cout << "long long: " << sizeof(long long) << " "
<< std::numeric_limits<long long>::min() << " "
<< std::numeric_limits<long long>::max() << std::endl;
}
Integer encoding
- Unsigned integers: simple conversion to base 2
- Signed integers: two's complement method
int a = 42, b = -42;
std::cout << std::bitset<32>(a) << std::endl;
std::cout << std::bitset<32>(b) << std::endl;
Floating-point values
- float (32 bits)
- double (64 bits)
- long double (platform dependent)
IEEE 754 norm
$r = (-1)^s \; m \; 2^{exponent - offset}$
- $s$: bit of sign
- $m$: bits of mantissa
- $exponent$: bits of exponent
| float | double | |
|---|---|---|
| sign | $1$ | $1$ |
| exponent | $8$ | $11$ |
| mantissa | $23$ | $52$ |
| lowest number | $1.4 10^{-45}$ | $4.9406564854124564 10^{-324}$ |
| highest number | $3.40282346 10^{38}$ | $1.7976931348623157 10^{308}$ |
Cast
- static_cast
- reinterpret_cast
- const_cast
- dynamic_cast
static_cast
- Syntax
static_cast<new_type>(expression)
- Example
int a = 1, b = 2;
std::cout << "integer division" << a/b << std::endl;
std::cout << "float division" << static_cast<float>(a)/b << std::endl;
// std::string *s = static_cast<std::string*>(&b); // compile error
Check if the cast is possible at compile time.
reinterpret_cast
- Syntax
reinterpret_cast<new_type>(expression)
- Example
int b = 2;
std::string *s = static_cast<std::string*>(&b);
std::cout << *s << std::endl; // segmentation fault
Instruct the compiler to treat expression as if it had the type new_type.
C-style cast
- Syntax
(new_type)expression
The compiler attempts to interpret it as the following cast
expressions, in this order:
const_cast<new_type>(expression)static_cast<new_type>(expression)reinterpret_cast<new_type>(expression)C-Style arrays
- Syntax:
double d[17];
int i[4];
d[0] = 1.2;
d[4] = 2.7;
- Statically allocated arrays
- Cannot be resized
- Have poor interfaces
Prefer std::array over C-style arrays
Arithmetic Operators
int a = 1, b = 2;
int c = -a;
int c2 = +a;
int d = a + b; int da = a; da += b;
int e = a - b; int ea = a; ea -= b;
int f = a * b; int fa = a; fa *= b;
int g = a / b; int ga = a; ga /= b;
int h = a % b; int ha = a; ha %= b;
Increment/decrement operators
int a = 2;
int b = a++;
int c = ++a;
int d = a--;
int e = --a;
Increment/decrement operators
int a = 2; // a = 2
int b = a++; // a = 3, b = 2
int c = ++a; // a = 4, b = 4
int d = a--; // a = 3, d = 4
int e = --a; // a = 2, e = 2
Comparison operators
bool r1 = a == b;
bool r2 = a != b;
bool r3 = a < b;
bool r4 = a ≤ b;
bool r5 = a > b;
bool r6 = a ≥ b;
Bitwise operators
int a = 1, b = 31;
int c = ~a;
int d = a & b; int da = a; da &= b;
int e = a | b; int ea = a; ea |= b;
int f = a ^ b; int fa = a; fa ^= b;
int g = a << 1; int ga = a; ga << 1;
int h = a >> 1; int ha = a; ha >> 1;
Bitwise operators
int a = 1, b = 31;
int c = ~a; // c = -2
int d = a & b; int da = a; da &= b; // d = 1
int e = a | b; int ea = a; ea |= b; // e = 31
int f = a ^ b; int fa = a; fa ^= b; // f = 30
int g = a << 1; int ga = a; ga << 1; // g = 2
int h = a >> 1; int ha = a; ha >> 1; // h = 0
Logical operations
bool a = true, b = false;
bool c = !a;
bool d = a && b;
bool e = a || b;
if and else
if(x > 0)
{
std::cout << "x is positive" << std::endl;
}
else if(x < 0)
{
std::cout << "x is negative" << std::endl;
}
else
{
std:cout << "x is 0" << std::endl;
}
Ternary operator
int c = (a > 0)? 10: -50;
while
#include <iostream>
int main(int argc, char* argv[])
{
int n = atoi(argv[1]);
std::cout << n << " ";
while (n != 1)
{
if (n&1)
{
n = (3*n + 1)/2;
}
else
{
n /= 2;
}
std::cout << n << " ";
}
std::cout << std::endl;
return 0;
}
- Pour $n = 12$: $12, 6, 3, 5, 8, 4, 2, 1$
- Pour $n = 19$: $19, 29, 44, 22, 11, 17, 26, 13, 20, 10, 5, 8, 4, 2, 1$
while
#include <iostream>
int main(int argc, char* argv[])
{
int n = atoi(argv[1]);
std::cout << n << " ";
while (n != 1)
{
if (n&1)
{
n = (3*n + 1)/2;
}
else
{
n /= 2;
}
std::cout << n << " ";
}
std::cout << std::endl;
return 0;
}
Collatz conjecture
do while
#include <iostream>
int main()
{
int counter = 5;
int factorial = 1;
do
{
factorial *= counter--;
} while (counter > 0);
std::cout << "factorial of 5 is " << factorial << std::endl;
}
for
#include <iostream>
int main()
{
double x[2] = {1, 3}, y[2] = {-2, .5};
double sum = 0;
for(std::size_t i = 0; i < 2; ++i)
{
sum += x[i]*y[i];
}
std::cout << sum << std::endl;
return 0;
}
break
#include <iostream>
int main()
{
for(int i = 10; i> 0; --i)
{
std::cout << i << std::endl;
if(i == 3)
{
std::cout << "countdown aborted" << std::endl;
break;
}
}
std::cout << "end of loop" << std::endl;
return 0;
}
continue
#include <iostream>
int main()
{
for(int i = 10; i> 0; --i)
{
if(i == 3)
{
continue;
}
std::cout << i << std::endl;
}
std::cout << "end of loop" << std::endl;
return 0;
}
switch
int i = std::rand() % 2;
switch(i)
{
case 0:
std::cout << "i is even" << std::endl;
break;
case 1:
std::cout << "i is odd" << std::endl;
default:
std::cout << "default case" << std::endl;
}
scope
#include <iostream>
int main()
{
int a = 10;
{
int b = 4096;
for(int i = 0; i < a; ++i)
{
b /= 2;
int c = b;
std::cout << c << std::endl;
}
std::cout << c << std::endl; // error: c is not accessible
int a = 5;
std::cout << a << std::endl;
}
std::cout << b << std::endl; // error: b is not accessible
return 0;
}
Readability
#include <iostream>
#include <cmath>
double f(std::size_t n)
{
double out = 0;
// start the loop
for (std::size_t i=0; i<n; ++i)
{
out += 1./n*std::sqrt(1 - (i*1./n*i*1./n));
}
return 4*out;
}
int main(int argc, char *argv[])
{
std::cout << f(1000) << std::endl;
return 0;
}
Readability
#include <iostream>
#include <cmath>
// Compute pi using the rectangle method
// to approximate the integral of 4*sqrt(1 - x^2)
// over [0, 1]
double compute_pi(std::size_t n)
{
double quarter_pi = 0;
double dx = 1./n;
for (std::size_t i=0; i<n; ++i)
{
double xi = i*dœx;
quarter_pi += h*std::sqrt(1 - xi*xi);
}
return 4*quarter_pi;
}
int main()
{
std::cout << compute_pi(1000) << std::endl;
return 0;
}